Hysteresis can be defined as the condition of a complex system in which the current state of the system tends to persist for a period after it has ceased to be the preferred, long-term stable state of the system. Peter Bernstein and Jared Bernstein have described the application of the idea of hysteresis to the financial markets and to more general economic systems.
In previous posts, we have discussed the theory of phase transitions, and how these theoretical concepts can be applied to understand the dynamics of complex systems including earthquakes and markets. An important idea was the concept of metastability, the temporary state of a system that is different from the long-term, preferred state of the system.
The idea of hysteresis is associated with metastability, but an important question relates to the process by which the system evolves into a metastable state. To answer this question, we return to the Landau Theory of phase transitions described previously.
We defined the order parameter of the system, together with a cost or fitness function. The order parameter describes the current state of the system, while the cost function defines the dynamics by which the system evolves. The system is driven by a persistent forcing f. For an earthquake fault, f is the plate tectonic forces.
For markets, f is the liquidity or money supply. For earthquakes, convective circulations deep within the earth’s mantle produce the tectonic forces that drive the plates. For markets, the federal reserve and other central banks supply the money necessary to grow the economy.
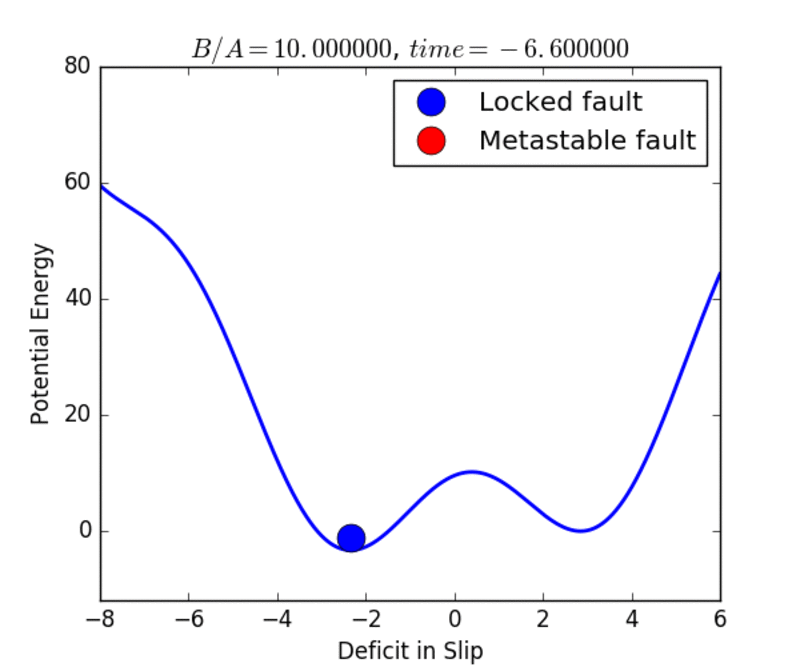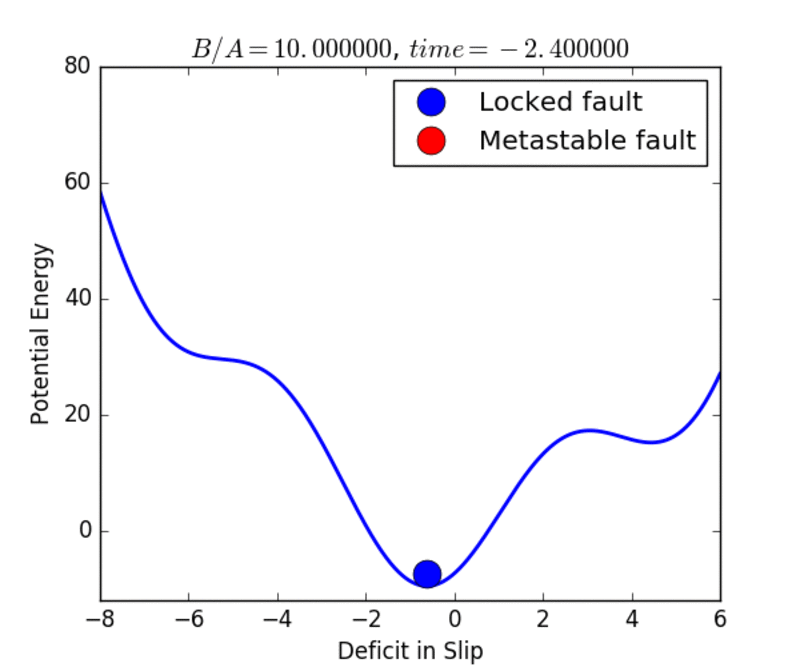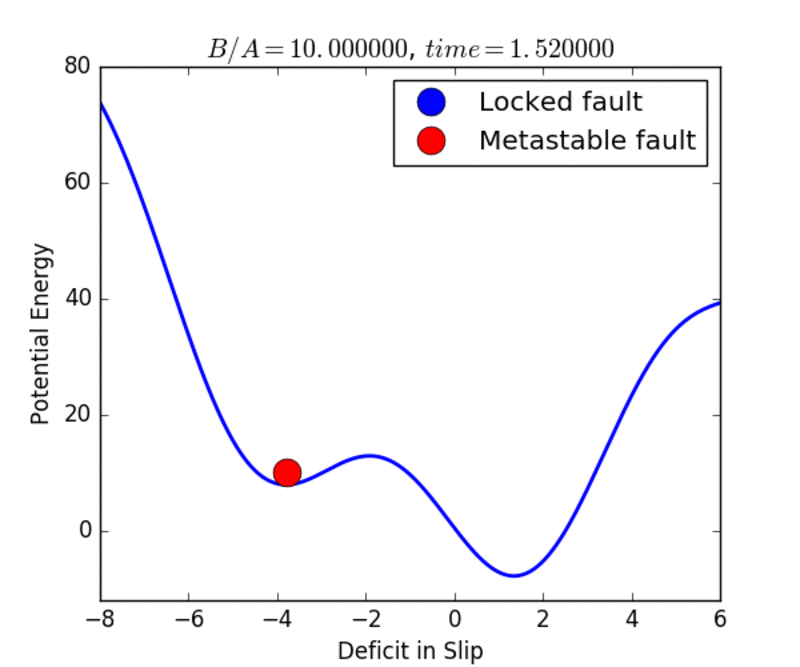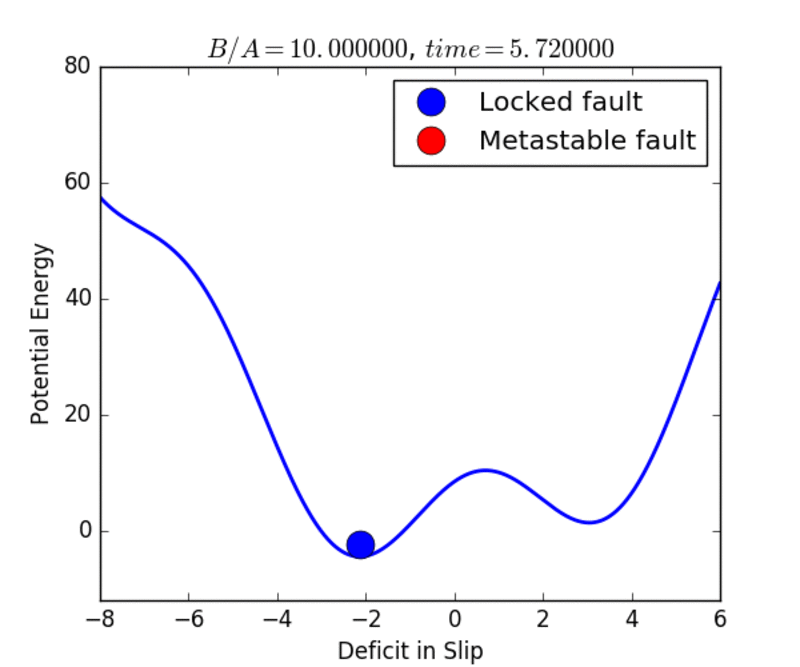
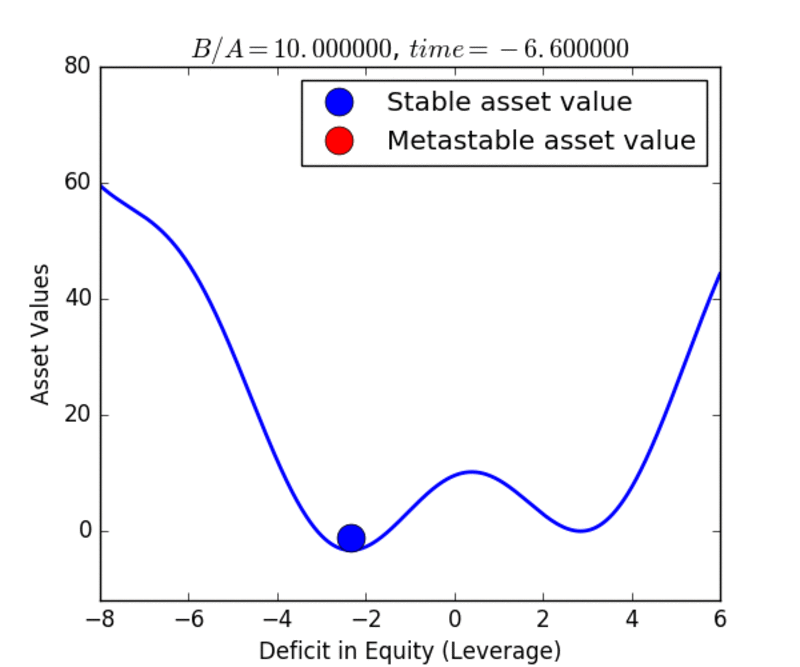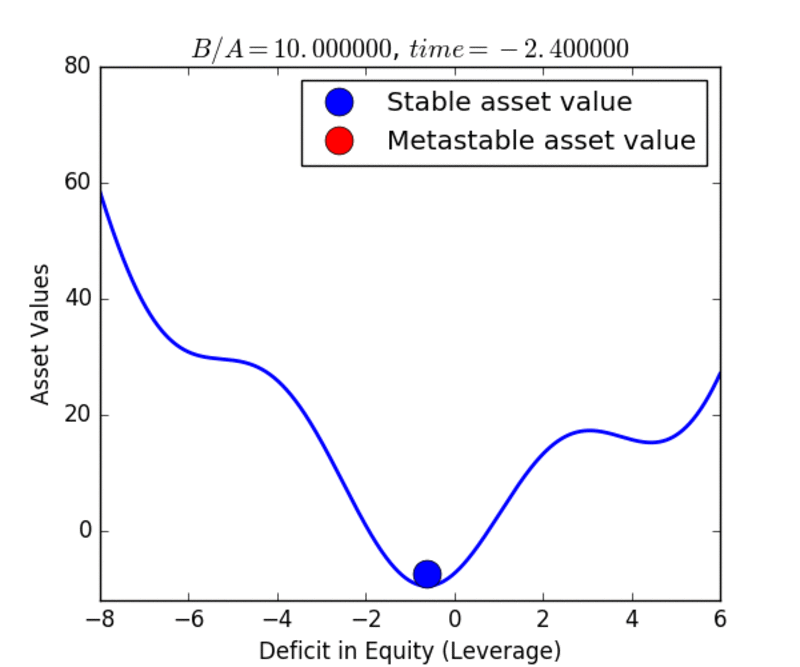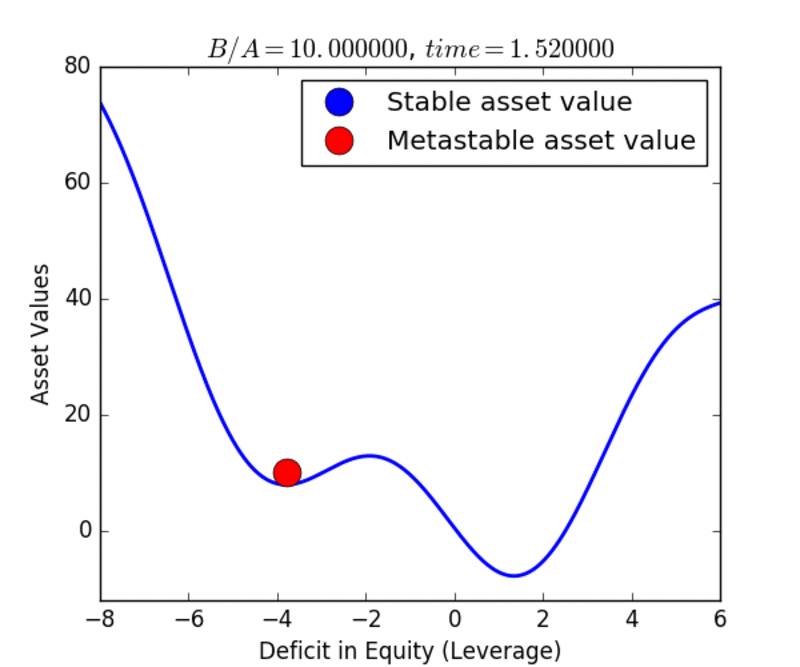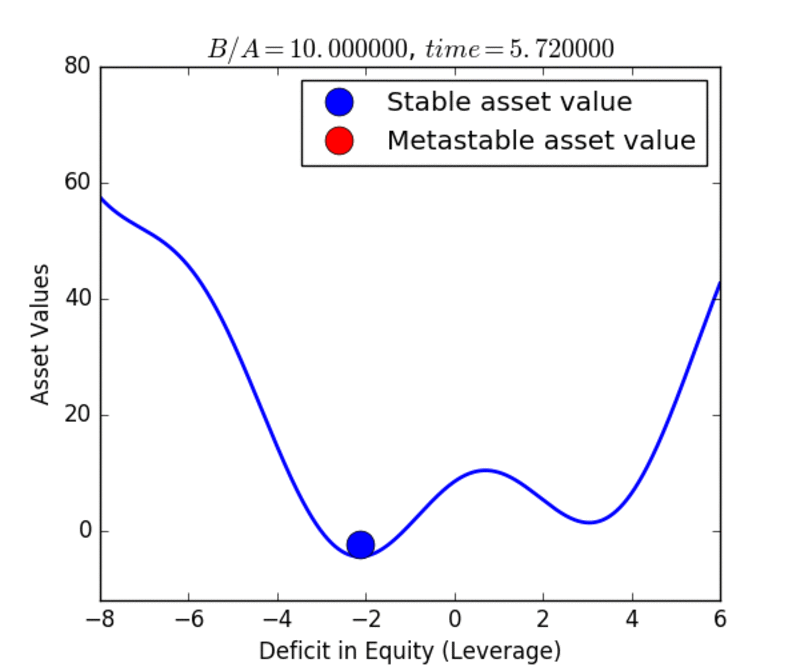
The Landau Theory postulates that the system evolves towards a state of minimum energy. This state can either be a local minimum, or a global minimum. An example for an earthquake fault is shown in the figure below , where there are two local minima. In this case, the order parameter is the deficit in slip on the earthquake fault.
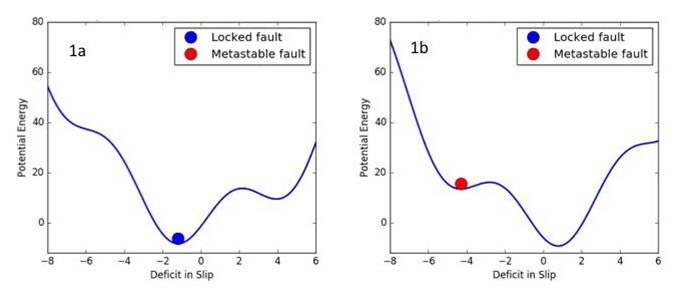
Because the earthquake fault is locked between earthquakes, the slip state on the fault lags behind the far-field displacement of the plates as the tectonic forces increase. The slip deficit is defined as the local current slip on the fault minus the far-field plate tectonic displacement. Thus as the plates move between earthquakes, the slip deficit becomes increasingly negative. The elastic potential energy stored by the fault also increases, much as the energy of a spring increases as it is stretched.
When the earthquake occurs, the potential energy is released, and the slip increases suddenly, meaning that the magnitude of the slip deficit decreases to zero. This process is illustrated in figures 1a and 1b, where figure 1a corresponds to the globally stable state, and figure 1b corresponds to the local metastable state. Hysteresis refers to the idea that the locked state of the fault tends to persist even after it is no longer the globally stable state, due to the potential energy barrier (“hill”) separating the metastable minimum (“higher valley”) from the lower, global minimum (“lower valley”).
The decay itself is ultimately caused either by random fluctuations (“noise”) inherent in the system, or by removal of the energy barrier, which may happen as the dynamical state evolves in time. As the energy barrier becomes smaller, the fluctuations have a greater chance of nucleating the transition. An important question relates to how the system evolves into the metastable state in the first place, a point that we discuss below. All these processes have been described mathematically in the statistical physics literature in great detail.
The same type of model can be applied to the markets, as shown in figures 2a and 2b. In this application, the earthquake cycle of “earthquake > locked fault > earthquake” is replaced by the business cycle of “recession > economic boom > recession”, or the leverage cycle of “market crash > inflated assets > market crash”. Here these economic systems would be driven by the increase in available liquidity arising from the increase in the money supply from the Federal Reserve, banks, the growth of GDP, and the velocity of money, among other factors.
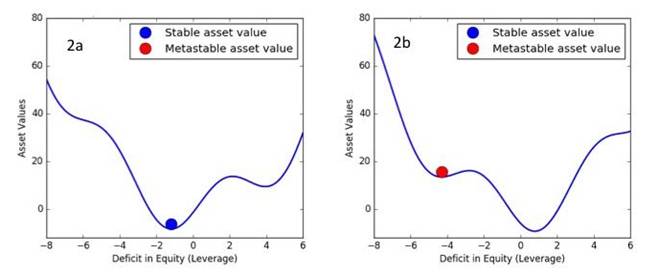
In the case of the markets, growth in the money supply drives the market cycle because liquidity increases most rapidly after the crash has occurred, and tends to persist too long when it is no longer needed. Late in the cycle, as the Federal Reserve removes liquidity, asset values can no longer be supported at their then-present levels.
In the view of economists such as John Geanokoplos of Yale University, moral hazard and other forms of risky behavior tend to grow throughout the market cycle, and in turn lead to an increase in leverage. Leverage is nothing more than an increase in the deficit in equity used to purchase an asset. Thus the increasing deficit in equity for markets corresponds to the increasing deficit in slip on earthquake faults leading up to the nucleation event (earthquake or market crash).
In the movies below, we show examples of the evolution of the earthquake and market cycles. At the beginning, the system occupies the global stable minimum, indicated by the blue color of the circle. Under the dynamics, the system evolves to produce a higher, metastable minimum as well. The red circle indicates that the state is metastable. The metastable state eventually decays and the system transitions to the stable state once again. The cycle continues as the a new metastable state is formed, and the system is lifted to higher energies and higher asset values. Hysteresis is associated with the fact that the system remains in an elevated potential energy or asset-valued state long after it should have transitioned. Read the Mathematical details.
Earthquakes
Markets
John Rundle is a Distinguished Professor of Physics and Geology at the University of California, Davis. We had the pleasure of meeting Professor Rundle through the Santa Fe Institute and were intrigued by his work on the dynamics of complex systems, specifically in the geosciences. His work on earthquake and hazard forecasting, and the similarities of these hazards to the financial markets expanded how we think about market movements and crashes.
Read his first post: Using Earthquakes to Understand Markets
Read his second post: Earthquakes and Markets: Stability
